The Linear Algebra Notes
Contents
- 0. Introduction
- 1. The Geometry of Linear Equations
- 2. Elimination
- 3. Multiplcation and Inverse Matrices
0. Introduction
This notes is about the fundamental of Linear Algebra lectured by MIT-1806.
You can right-click formulas to check their $$\LaTeX$$ codes or left-click pictures or animations to check their python codes which depend on matplotlib and manim.
If the LaTeX formulas cannot be displayed correctly, try refreshing the page.
Some of the media are from the Internet. You can find them in reference.
Here are wonderful resources which is useful for learning linear algebra:
- Essence of linear algebra by 3Blue1Brown [Official | Youtube | Chinese translation on bilibili]
1.The Geometry of Linear Equations
The fundamental problem of linear algebra is to solve a system of linear equations.
The normal case is n equations with n unknowns. For example:
A simple example of two equations with two unknowns
$$
\begin{cases}
\ 2x&-y&=0 \\ -x&+2y&=3
\end{cases}
$$
We can use matrix and vector to express it:
$$
\begin{equation}
\begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix}
\begin{bmatrix} x \\ y \end{bmatrix} =
\begin{bmatrix} 0 \\ 3 \end{bmatrix}
\end{equation}
$$
Using three letters to express this three matrix:
$$ A\mathbf{X}=b $$
A is coefficient matrix. $X$ is vector of unknowns. $b$ is vector of the right-hand numbers of equations.
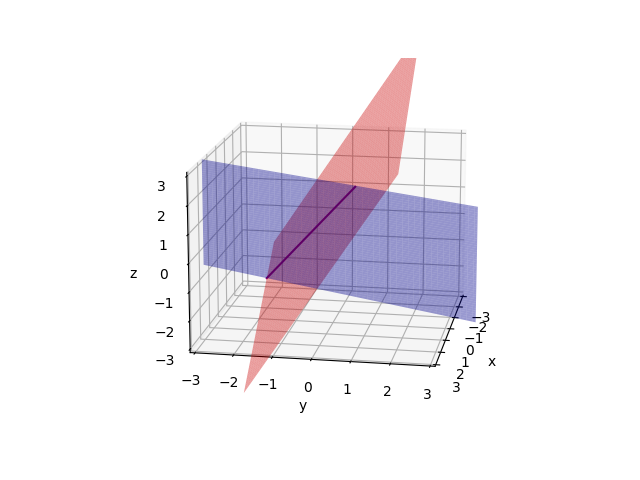
We can draw the row pictures of equations on a xy plane. Obviously They are two lines. all the points in each line are solutions of equation.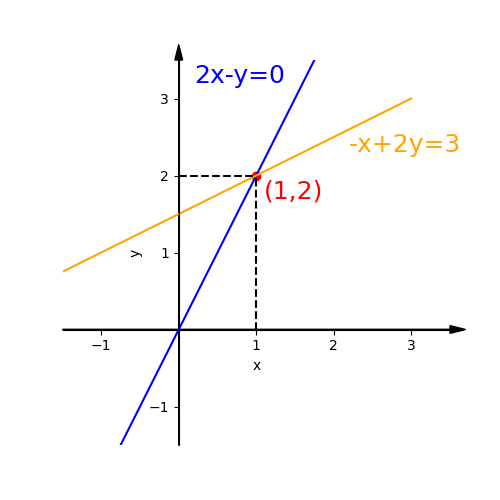
Then the column pitures:
Focusing on the columns of matrix, we can get this:
$$
\begin{equation}
x \begin{bmatrix} 2 \\ -1 \end{bmatrix} + y
\begin{bmatrix} -1 \\ 2 \end{bmatrix} =
\begin{bmatrix} 0 \\ 3 \end{bmatrix}
\end{equation}
$$
This equation is asking us to find the x and y to combine the vector $x\begin{bmatrix} 2 \\ -1 \end{bmatrix}$ and the vector $y\begin{bmatrix} -1 \\ 2 \end{bmatrix}$ to get the vector $\begin{bmatrix} 0 \\ 3 \end{bmatrix}$. That is the linear combination we need to find.
Draw three vectors mentioned above. We already know the right x and y. So we can get the red vector when combining 2 green vectors and 1 blue vector.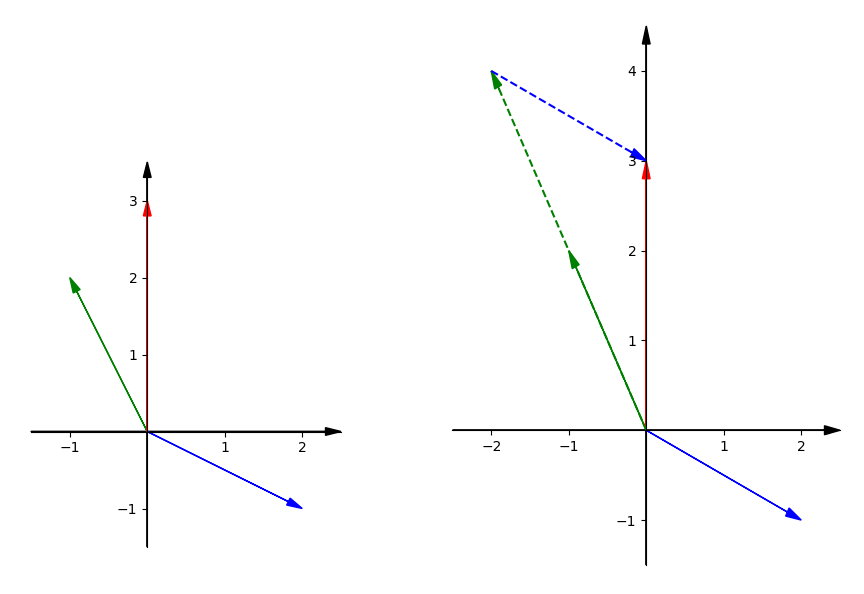
If we change the x and y, we can find that the new vector is able to fill all the xy plane. It means we can produce a vector point at everywhere in this plane.
3 equations with 3 unknowns
Now let’s see the 3x3 case.
$$
\begin{cases}
2x & -y & &= 0 \\
-x & +2y & -z &= -1 \\
& -3y & +4z &= 4
\end{cases}
$$
Similarly, We can use $ A\mathbf{X}=b $ to describe it.
$$
\begin{equation}
A=\begin{bmatrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -3 & 4 \end{bmatrix},
\mathbf{X}=\begin{bmatrix} x \\ y \\ z \end{bmatrix},
b=\begin{bmatrix} 0 \\ -1 \\ 4 \end{bmatrix}
\end{equation}
$$
See the row pictures:
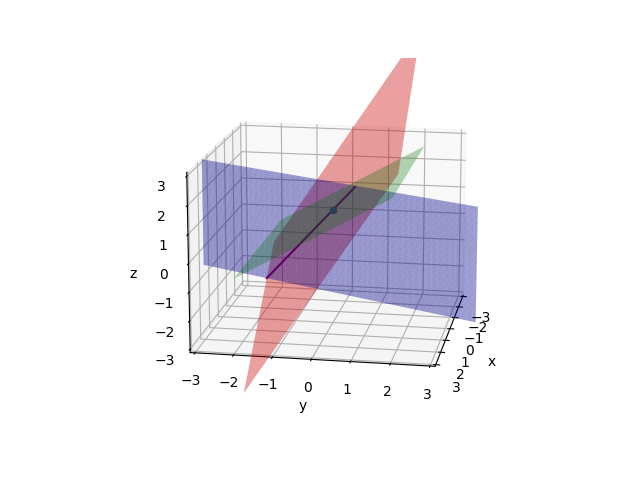
Firstly draw two planes(2x-y=0 and -x+2y-z=-1). These planes meet in a line.
Then draw the third plane(-3y+4z=4).They meet in a point(0, 0, 1). And this point is solution of equations.
This row picture is complicated. In 4x4 case or higher dimensions, the problem will be more complex and we cannot draw a picture like this.
Those three planes are not parallel, and they are not special.
Then column pictures:
$$
\begin{equation}
x \begin{bmatrix} 2 \\ -1 \\ 0 \end{bmatrix} +
y \begin{bmatrix} -1 \\ 2 \\ -3 \end{bmatrix} +
z \begin{bmatrix} 0 \\ -1 \\ 4 \end{bmatrix} =
\begin{bmatrix} 0 \\ -1 \\ 4 \end{bmatrix}
\end{equation}
$$
Solve this equation so we can get the linear combination of three vectors. Each vector is a three dimensions one.
Then we can get $x=0, y=0, z=1$.
If we change the $b$. For example $b = x\begin{bmatrix} 1 \\ 1 \\ -3 \end{bmatrix}$. We can also get the linear combination $x=1, y=1, z=0$.
Can every equation be solved?
Think about this:
Can I solve $A\mathbf{X}=b$ for every $b$?
If we change the x, y and z in this example, we can find that the new vector produced can point at everywhere in this space.
So in linear combination words, the problem is
Do the linear combinations of the columns fill three dimensional space?
In this example, for the matrix $A$, the answer is yes.
Imagine that if three vectors are in the same plane, and the vector $b$ is out of this plane. Then the combination of three vectors is impossible to produce $b$. In this case, $A$ is called singular matrix. And $A$ would be not invertible.
How to multiply a matrix by a vector?
Column operation: $\begin{equation}
\begin{bmatrix} a & b \\ c & e \end{bmatrix}
\begin{bmatrix} x \\ y \end{bmatrix} =
x\begin{bmatrix} a \\ c \end{bmatrix} +
y\begin{bmatrix} b \\ d \end{bmatrix}
\end{equation}$
See what happens to $\begin{equation}
\begin{bmatrix} \color{green}3 & \color{red}1 \\ \color{green}1 & \color{red}2 \end{bmatrix}
\begin{bmatrix} \color{orange}-1 \\ \color{orange}2 \end{bmatrix} =
\begin{bmatrix} \color{orange}-1 \\ \color{orange}3 \end{bmatrix}
\end{equation}$
2. Elimination
Now let’s think about how to solve equations.
For example:
$$
\begin{cases}
x & +2y & +z &= 2 \quad &(1) \\
3x & +8y & +z &= 12 \quad &(2) \\
&\ \ 4y & +z &= 2 \quad &(3)
\end{cases}
$$
And the matrix $A=\begin{bmatrix} 1 & 2 & 1 \\ 3 & 8 & 1 \\ 0 & 4 & 1 \end{bmatrix}$.
If we accept an equation, we can accept that if it multiplies a number or add a number.
For example:
If $$ x + 2 = 3y $$, $$ 2 \times (x + 2) = 2 \times 3y $$ can be accepted too. So does $$ 2 \times (x + 2) + z = 2 \times 3y + z $$.
So if (1) times a number and then add to (2), it won’t change the solutions of equations. If (1) times $-3$ and then add to (2), we will get $$ 2y - 2z = 6$$, the $x$ is knocked out. This method is called elimination and it is a common way to solve equations.
If speaking in matrix words, this matrix operation is:
$$
\begin{bmatrix} \boxed{\color{red}{1}} & 2 & 1 \\ 3 & 8 & 1 \\ 0 & 4 & 1 \end{bmatrix}
\xrightarrow{row_2 \ - \ 3row_1}
\begin{bmatrix} \boxed{\color{red}{1}} & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 4 & 1 \end{bmatrix}
$$
The boxed and red number 1 is the key number of this step. We call it pivot.
What about the right-hand vector $b$? Actually Matlab finishes up the left side $A$ and then go back to the right side $b$. So we can do with it later.
In (3), the coefficent of $x$ is already 0. If not, we can eliminate it in the same way.
Next step we can do it again to eliminate the $y$ in (3). In this step the second pivot is 2. Similarly, the thrid pivot is 5
$$
\begin{bmatrix} \boxed{\color{red}{1}} & 2 & 1 \\ 0 & \boxed{\color{green}{2}} & -2 \\ 0 & 4 & 1 \end{bmatrix}
\xrightarrow{row_3 \ - \ 2row_2}
\begin{bmatrix} \boxed{\color{red}{1}} & 2 & 1 \\ 0 & \boxed{\color{green}{2}} & -2 \\ 0 & 0 & \boxed{\color{blue}{5}} \end{bmatrix}
$$
In last step, we get a upper triangular matrix $U=\begin{bmatrix} 1 & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 0 & 5 \end{bmatrix}$
So the purpose of elimination is to get from $A$ to $U$.
Note that pivots cannot be 0.
When does elimination fail?
If the firse pivot is 0, does elimination fail? No. In last example, if we exchange the position of (1) and (3), the first pivot will be 0. But the solution of equations won’t be changed. So if the pivots is 0, try exchanging rows.
If $A=\begin{bmatrix} 1 & 2 & 1 \\ 3 & 8 & 1 \\ 0 & 4 & \boxed{-4} \end{bmatrix}$, in last step we will get a matrix $\begin{bmatrix} 1 & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 0 & 0 \end{bmatrix}$. Then the third pivot is 0. It means the equations have no solution. The elimination meets its failure. In this case matrix $A$ would have not been invertible.
Back subtitution
Consider $b$. We can place it to the extra column of $A$ to get a Augmented Matrix.
$$
[A|b]=
\begin{bmatrix} \begin{array}{ccc | c}
1 & 2 & 1 & 2 \\ 3 & 8 & 1 & 12 \\ 0 & 4 & 1 & 2 \\
\end{array} \end{bmatrix}
$$
Then we do the same operations with this matrix:
$$
\begin{bmatrix} \begin{array}{ccc | c}
1 & 2 & 1 & 2 \\ 3 & 8 & 1 & 12 \\ 0 & 4 & 1 & 2 \\
\end{array} \end{bmatrix}
\xrightarrow{row_2 \ - \ 3row_1}
\begin{bmatrix} \begin{array}{ccc | c}
1 & 2 & 1 & 2 \\ 0 & 2 & -2 & 6 \\ 0 & 4 & 1 & 2 \\
\end{array} \end{bmatrix}
\xrightarrow{row_3 \ - \ 2row_2}
\begin{bmatrix} \begin{array}{ccc | c}
1 & 2 & 1 & 2 \\ 0 & 2 & -2 & 6 \\ 0 & 0 & 5 & -10 \\
\end{array} \end{bmatrix}
$$
$b$ will be a new vector $c=\begin{bmatrix} 2 \\ 6 \\ -10 \end{bmatrix}$
And we can finally get new equations:
$$
\begin{cases}
x & +2y & +z &= 2 \\
&\ \ \ 2y & -2z &= 6 \\
& &\ \ \ 5z &= -10
\end{cases}
$$
Those are the equations $ U \mathbf{X} = c $.
And we can easily figure out that $z=-2, y=1, x=2$.
Using matrices multiplication to describe the matrices operations
How to use matrix language to describe this operation?
Last lecture we have learnt how to multiply a matrix by a column vector. Here is how to multiply a row vector by a matrix.
$$\begin{equation}
\begin{bmatrix} x & y & z \end{bmatrix}
\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} =
x \times \begin{bmatrix} a & b & c \end{bmatrix} + y \times \begin{bmatrix} e & f & g \end{bmatrix} + z \times \begin{bmatrix} h & i & j \end{bmatrix}
\end{equation}$$
This is a row operation.
So if the row vector is on the left, the matrix does row operation. If the column vector is on the right, the matrix does column operation.
If a 3x3 matrix is multipied by $I=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$, the matrix would not be changed. $AI = IA = A$. It means this matrix operation do nothing with the matrix $A$. And the matrix $I$ is called identity matrix.
Step 1: Subtract $3 \times row_1$ from $row_2$
$$
\begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} 1 & 2 & 1 \\ 3 & 8 & 1 \\ 0 & 4 & 1 \end{bmatrix} =
\begin{bmatrix} 1 & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 4 & 1 \end{bmatrix}
$$
What does this multiplication means? Look at the row 2 of the left matrix. How does it affect the second matrix?
We know $\begin{equation}
\begin{bmatrix} -3 & 1 & 0 \end{bmatrix}
\begin{bmatrix} 1 & 2 & 1 \\ 3 & 8 & 1 \\ 0 & 4 & 1 \end{bmatrix} =
-3 \times \begin{bmatrix} 1 & 2 & 1 \end{bmatrix} + 2 \times \begin{bmatrix} 3 & 8 & 1 \end{bmatrix} + 0 \times \begin{bmatrix} 0 & 4 & 1 \end{bmatrix} =
\begin{bmatrix} 0 & 2 & -2 \end{bmatrix}
\end{equation}$
So $\begin{matrix}-3 & 1 & 0\end{matrix}$ means $-3 \times row_1 + 1 \times row_2 + 0 \times row_3$ produces the second row $\begin{matrix}0 & 2 & -2\end{matrix}$ of new matrix.
And the simple matrix $E_{21}=\begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $ which is used to operate the matrix $A$ is called Elementary Matrix.
$E_{21}$ means it will change the number to 0 on the position of row 2 and column 1.
Step 2: Subtract $2 \times row_2$ from $row_3$.
$$
\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -2 & 1 \end{bmatrix}
\begin{bmatrix} 1 & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 4 & 1 \end{bmatrix} =
\begin{bmatrix} 1 & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 0 & 5 \end{bmatrix}
$$
We use $E_{32}$ to represent the left matrix.
These two operations can be written as $E_{32}(E_{21}A)=U$
We use two elementary matrices to produce the matrix $U$. Can we use only one matrix to do that? The answer is yes.
$$E_{32}(E_{21}A)==(E_{32}E_{21})A=EA=U,\\
\mathrm{composition\ matrix}\ E=E_{32}E_{21}$$
This method to change the parentheses is called associative law.
The composition matrix is the multiplication of two matrices. It mix two transformations into one. And this is the meaning of matrices multiplication.
Permutation Matrix
Another elementary matrix that exchanges two rows is called Permutation Matrix.
For example, if we want to exchange two rows of $\begin{bmatrix} a & b \\ c & d \end{bmatrix}$, what matrix can we use?
$$
\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}
\begin{bmatrix} a & b \\ c & d \end{bmatrix} =
\begin{bmatrix} c & d \\ a & b \end{bmatrix}
$$
How if we want to exchange two columns of matrix? Put the permutation matrix on the right.
$$
\begin{bmatrix} a & b \\ c & d \end{bmatrix}
\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} =
\begin{bmatrix} b & a \\ d & c \end{bmatrix}
$$
According to this two examples, we know that $AB$ is not the same as $BA$. So the order of the matrices multiplication is important.
How to get from U back to A
See the matrix $\begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$. It subtract $3 \times row_1$ from $row_2$. How to undo this operation?
We know $IA=A$. So if we can find out a matrix $E^{-1}$ so that $E^{-1}E=I$, then $E^{-1}EA=IA=A$.
The matrix $E^{-1}$ is called $E$ inverse.
$$
\begin{bmatrix} 1 & 0 & 0 \\ 3 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}=
\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
$$
3.Multiplication and Inverse Matrices
We use $a_{ij}$ to describe the element of $A$ on line i, column j.
When do A and B allowed to be multiplied
$$
A_{\color{blue}{m}\times\color{red}{k}}
B_{\color{red}{k}\times\color{green}{n}}=
C_{\color{blue}{m}\times\color{green}{n}}
$$
That means the multiplication must be a left matrix with k columns and a right matrix with k rows.
If the left matrix has m rows and the right matrix has n columns, the result will have m rows and n columns.
5 ways to do multiplication with matrices
1. Dot production of vector [$row_i$] and vector [$colomn_j$]
$$
\begin{bmatrix}
& & & \vdots \\
a_{i1} & a_{i2} & \cdots & a_{ik} \\
& & & \vdots
\end{bmatrix}
\begin{bmatrix}
& b_{1j} & \\
& b_{2j} & \\
& \vdots & \\
\cdots & b_{kj} & \cdots
\end{bmatrix}=
\begin{bmatrix}
& \vdots & & \\
\cdots & c_{ij} & \cdots & \\
& \vdots & &
\end{bmatrix}
$$
$$
c_{ij}=
\begin{bmatrix}a_{i1} & a_{i2} & \cdots & a_{ik}\end{bmatrix} \cdot
\begin{bmatrix}b_{1j}\\b_{2j}\\\vdots\\b_{kj}\end{bmatrix}
=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots+a_{ik}b_{kj}
=\sum^{k}_{p=1}a_{ip}b_{pj}
$$
2. Each column of C is the linear combination of A
$$
\begin{bmatrix}
A_{col_1} & A_{col_2} & \cdots & A_{col_k}
\end{bmatrix}
\begin{bmatrix}
\cdots & b_{1j} & \cdots \\
\cdots & b_{2j} & \cdots \\
\cdots & \vdots & \cdots \\
\cdots & b_{kj} & \cdots
\end{bmatrix}=
\begin{bmatrix}
\cdots & (b_{1j}A_{col_1} & b_{2j}A_{col_2} & \cdots & b_{kj}A_{col_k}) & \cdots
\end{bmatrix}
$$
3. Each row of C is the linear combination of B
$$
\begin{bmatrix}
\vdots & \vdots & \vdots & \vdots \\
a_{i1} & a_{i2} & \cdots & a_{ik} \\
\vdots & \vdots & \vdots & \vdots
\end{bmatrix}
\begin{bmatrix}
B_{row_1} \\ B_{row_2} \\ \vdots \\ B_{row_k}
\end{bmatrix}=
\begin{bmatrix}
\vdots \\
(a_{i1}B_{row_1} + a_{i2}B_{row_2} + \cdots + a_{ik}B_{row_k}) \\
\vdots \\
\end{bmatrix}
$$
4. Multiply columns of A by rows of B
$$
\begin{bmatrix}
A_{col_1} & A_{col_2} & \cdots & A_{col_k}
\end{bmatrix}
\begin{bmatrix}
B_{row_1} \\ B_{row_2} \\ \vdots \\ B_{row_k}
\end{bmatrix}=
A_{col_1}B_{row_1}+A_{col_2}B_{row_2}+\cdots+A_{col_k}B_{row_k}
$$
5. Block Multiplication
$$
\begin{bmatrix}\begin{array}{c | c}
A_1 & A_2 \\ \hline{} A_3 & A_4
\end{array}\end{bmatrix}
\begin{bmatrix}\begin{array}{c | c}
B_1 & B_2 \\ \hline{} B_3 & B_4
\end{array}\end{bmatrix}=
\begin{bmatrix}\begin{array}{c | c}
A_1B_1+A_2B_3 & A_1B_2+A_2B_4 \\ \hline{}
A_3B_1+A_4B_3 & A_3B_2+A_4B_4
\end{array}\end{bmatrix}
$$
What does the matrices multiplication mean?
Last lecture we have learnt that the matrices multiplication mixes two transformations into one. If the rotation matrix $A=\begin{bmatrix}0&-1\\1&0\end{bmatrix}$ and the shear matrix $B=\begin{bmatrix}1&1\\0&1\end{bmatrix}$, then the composition matrix $C=BA=\begin{bmatrix}1&-1\\1&0\end{bmatrix}$. See what happened in this video:
What if $D=AB$?
We can see that $AB \neq BA$ in this example.
Inverse (Square Matrices)
If matrix $A$ is invertible, then there is another matrix called $A$ inverse. And it multiplies $A$ produces $I$(Identity).
If left inverse exists, then also the matrix on the right can get identity. That means the left inverse of square matrix equals the right inverse.
$$ A^{-1}A = AA^{-1} = I $$
For rectangular matrices the left inverse isn’t the right inverse because the shape is not allow the multiplication.
When does inverse exist
Not all square matrices have inverses. The matrices which have inverses are called invertible or non-singular matrices.
For singular matrices, they have no inverses. And their determinant is 0. And we can find a non-zero vector $x$ with $Ax=0$.
For example, if $A=\begin{bmatrix}1 & 3 \\ 2 & 6\end{bmatrix}$, the columns of A are both on the same line. So every linear combination is on that line and is impossible to get $\begin{bmatrix}1 \\ 0\end{bmatrix}$ or $\begin{bmatrix}0 \\ 1\end{bmatrix}$. That means there is no matrix can be multiplied by $A$ to get $I$.
If $x=\begin{bmatrix}3 \\ -1\end{bmatrix}$, then $Ax=\begin{bmatrix}1 & 3 \\ 2 & 6\end{bmatrix}\begin{bmatrix}3 \\ -1\end{bmatrix}=0$.
Proof: Suppose that we can find a non-zero vector $x$ with $Ax=0$ and A is invertible, then $A^{-1}Ax=Ix=x=0$. So the assumption is false.
How to get $A^{-1}$
$A=\begin{bmatrix}1 & 3 \\ 2 & 7\end{bmatrix}$ for example, suppose $A^{-1}=\begin{bmatrix}a & b \\ c & d\end{bmatrix}$, then $\begin{bmatrix}1 & 3 \\ 2 & 7\end{bmatrix}\begin{bmatrix}a & c \\ b & d\end{bmatrix}=\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}$. We can get a system of equations:$
\begin{cases}
\begin{bmatrix}1 & 3 \\ 2 & 7\end{bmatrix}\begin{bmatrix}a \\ b\end{bmatrix}=\begin{bmatrix}1 \\ 0\end{bmatrix} \\
\begin{bmatrix}1 & 3 \\ 2 & 7\end{bmatrix}\begin{bmatrix}c \\ d\end{bmatrix}=\begin{bmatrix}0 \\ 1\end{bmatrix}
\end{cases}$
Gauss-Jordam(Solve 2 equations at once):
Stick the I to the right of A, making it an augmented matrix:$
[A|I]=
\begin{bmatrix}\begin{array}{cc | cc}
1 & 3 & 1 & 0 \\
2 & 7 & 0 & 1
\end{array}\end{bmatrix}$.
Then transform it into $[I|E]$ by elimination.
$$
\begin{bmatrix}\begin{array}{cc | cc}
1 & 3 & 1 & 0 \\
2 & 7 & 0 & 1
\end{array}\end{bmatrix}
\xrightarrow[E_{21}]{row_2 \ - \ 2row_1}
\begin{bmatrix}\begin{array}{cc | cc}
1 & 3 & 1 & 0 \\
0 & 1 & -2 & 1
\end{array}\end{bmatrix}
\xrightarrow[E_{12}]{row_1 \ - \ 3row_2}
\begin{bmatrix}\begin{array}{cc | cc}
1 & 0 & 7 & -3 \\
0 & 1 & -2 & 1
\end{array}\end{bmatrix}
$$
Look at the left side. The matrix operation $E=E_{21}E_{12}$ makes $A$ become $I$. So $EA=I$. And the right side $I$ becomes $E$ because $EI=E$. Then $E=A^{-1}$.